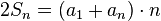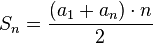Progressões Aritmética e Geométrica
Este tópico engloba recursos que abordam progressão aritmética, progressão geométrica e outras sequências numéricas acessíveis em nível de Ensino Médio.
Corrida ao 100
Mídia: experimento
Este experimento propõe um jogo. A estratégia vencedora desse jogo pode ser explorada como uma progressão aritmética.
Quadrado mágico aditivo
Mídia: experimento
Este experimento usa um antigo passatempo - o quadrado mágico - para tratar de conceitos de progressão aritmética.
Quadrado mágico multiplicativo
Mídia: experimento
Este experimento usa um antigo passatempo - o quadrado mágico - para tratar de conceitos de progressão geométrica.
O Quadrado de Koch
Mídia: experimento
Este experimento mostra alguns estudos possíveis ao observarmos padrões que emergem de um fractal.
Fonte :http://www.mais.mat.br/wiki/Progress%C3%B5es_aritm%C3%A9tica_e_geom%C3%A9trica
http://www.sbem.com.br/files/viii/pdf/03/MC41839641053.pdf
Somas Cruzadas
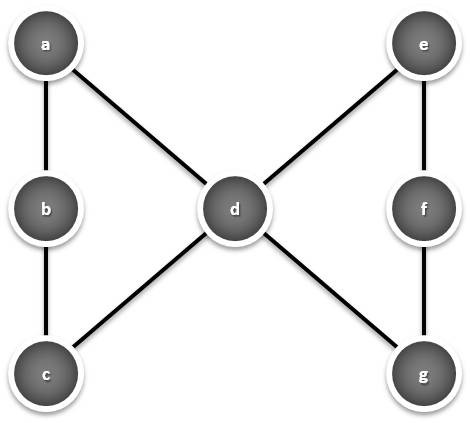
Efetuar atividades de ludicidade matemática envolvendo números posicionados em formas geométricas, tem sido um hábito recorrente deste blog. Desta vez, a figura escolhida engloba dois triângulos com um vértice comum:
A tarefa consiste em posicionar os primeiros sete números naturais, todos e apenas uma vez, no lugar das letras, de modo que: (a + b + c = a + d + g = e + f + g = c + d + e.
Ora bem, as condições do enunciado da tarefa levam a concluir que a soma dos quatro números pertencentes a cada triângulo terá de ser a mesma, isto é: a + b + c + d = d + e + f +g. Por outro lado, a soma dos sete valores envolvidos na tarefa é 28, pois 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7. Logo, se se excluir o valor comum (d), a soma dos seis números restantes terá de ser um valor par, para que possibilite duas metades inteiras de igual valor numérico, pois a + b + c = e + f + g. Sendo assim, existem três possibilidades de isso ocorrer:
- atribuir à letra "d" o valor 2, resultando uma soma 26, subdividida em duas somas de valor 13;
- atribuir à letra "d" o valor 4, resultando uma soma 24, subdividida em duas somas de valor 12;
- atribuir à letra "d" o valor 6, resultando uma soma 22, subdividida em duas somas de valor 11.
Resta, agora, testar se para cada caso os seis números sobrantes se dividem exactamente nas duas somas de igual valor numérico:
- 1º caso: 13 = 7 + 5 + 1 e 13 = 6 + 4 + 3;
- 2º caso: 12 = 7 + 3 + 2 e 12 = 6 + 5 + 1;
- 3º caso: 11 = 7 + 3 + 2 e 11 = 5 + 4 + 2.
Testemos cada caso na respectiva figura:
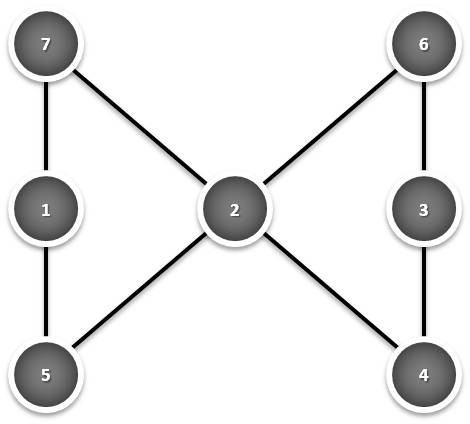
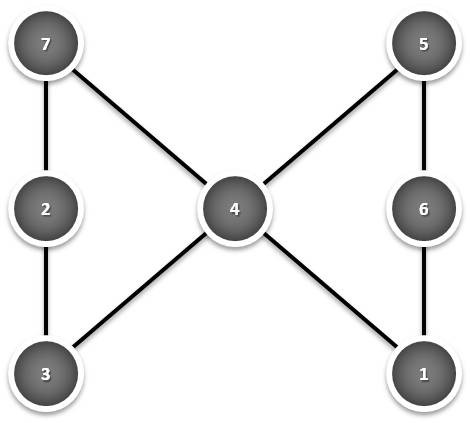
1º caso:
Verifica-se, pois que 7 + 1 + 5 = 7 + 2 + 4 = 5 + 2 + 6 = 6 + 3 + 4 = 13.
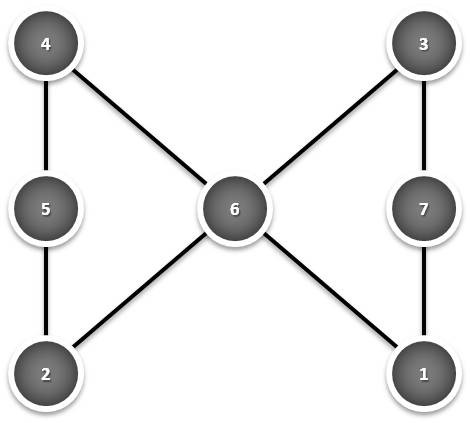
2º caso:
Neste caso, confirma-se que: 7 + 2 + 3 = 7 + 4 + 1 = 3 + 4 + 5 = 5 + 6 + 1 =12.
3º caso:
Veja-se que neste caso: 4 + 5 + 2 = 4 + 6 + 1 = 2 + 6 + 3 = 3 + 7 + 1=11.
A tarefa revelou, pois, uma natureza aberta, por permitir mais do que uma solução.
Imagine-se, agora, um estudo envolvendo os sete primeiros múltiplos naturais do 5 e, de seguida, os sete primeiros múltiplos naturais do 10. Como se posicionariam os números no caso de ser possível obedecer às premissas da tarefa inicial?
Eis uma possível solução, tirando partido, por exemplo, da ordem posicional dos elementos envolvidos no 1º caso da tarefa inicial deste artigo:
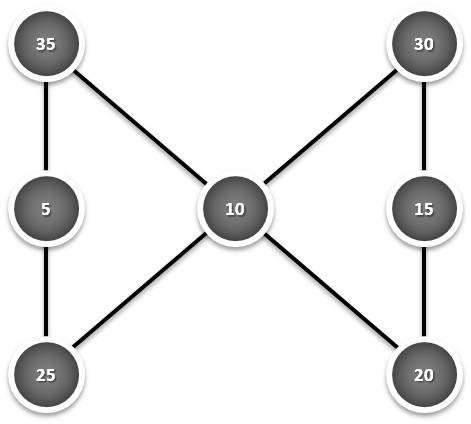
Múltiplos do 5:
|
Múltiplos do 10:
|
|
|
|
Note-se que a soma em qualquer linha da figura da esquerda é sempre 65 e nas da direita é sempre o seu dobro: 130.
Em contexto de sala de aula, seria desejável que os alunos conseguissem estabelecer uma relação entre o menor dos números envolvidos e a soma mágica a obter. Note-se que a iniciar em 5, e com os múltiplos naturais do 5, a soma foi 65; a iniciar em 10, e com os múltiplos naturais do 10, a soma foi 130, ou seja 65 + 1 x 65. Qual será a soma quando se inicia no valor 20, usando os sete primeiros múltiplos naturais deste valor?
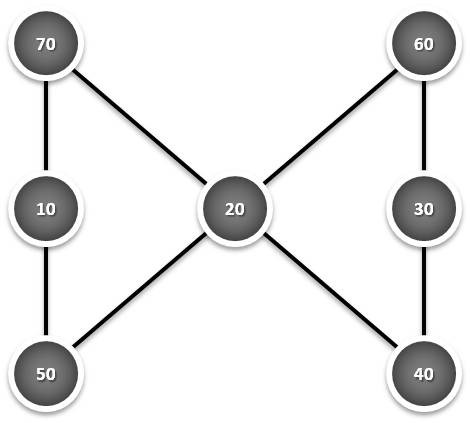
Ora, seria desejável que os alunos inferissem a lei geral que permite obter uma qualquer soma (s) a partir dos sete primeiros múltiplos de números, que sejam múltiplos naturais do cinco. Assim, s = 65 + (n - 1) x 65, sendo "n" o número de ordem, múltiplo natural do 5. Logo, para n = 20 estaremos na presença do quarto múltiplo natural do 5 e a soma respectiva será a seguinte: s = 65 + (4 - 1) x 65 = 65 + 3 x 65 = 260. Confirmemos com a figura:
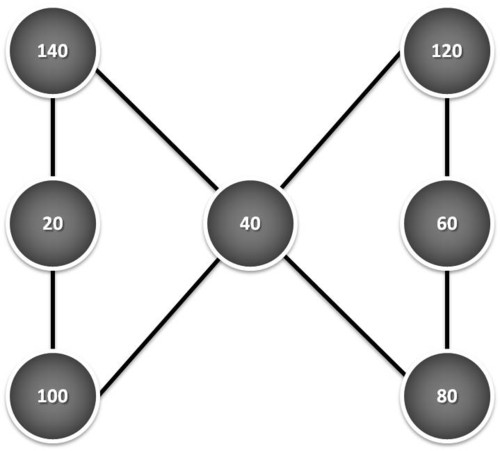
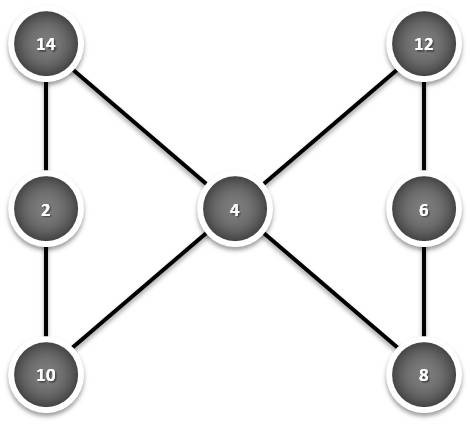
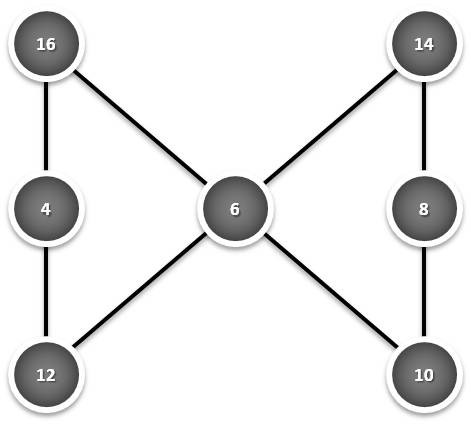
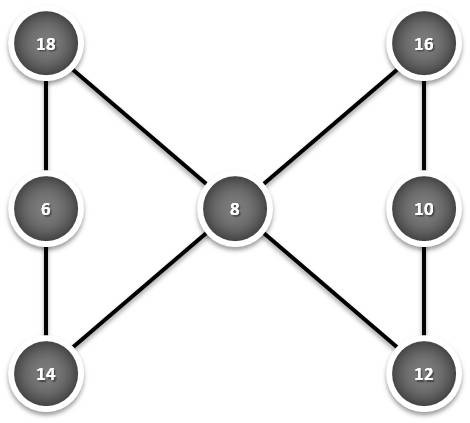
Analise em conjunto as três figuras seguintes, encontre uma lei geral que descreva matematicamente a soma obtida em função do respectivo menor valor envolvido em cada uma delas e projecte a possível soma de uma nova figura como estas, iniciada pelo valor 20:
Latas em Progressão Aritmética
Uma pesquisa sobre a biografia de Friedrich Gauss leva-nos a um interessante episódio com mais de 200 anos, sendo já uma importante referência na história da matemática. Conta-se que este prestigioso matemático alemão, ao começar a dar os seus primeiros passos académicos, surpreendeu o seu professor quando sujeito a uma actividade matemática que consistia em determinar a soma de todos os números inteiros de 1 a 100.
Sendo uma tarefa muito penosa para todos os seus colegas, Gauss muito rapidamente, colocou em cima da secretária do professor a sua ardósia com a conclusão da tarefa. Sentindo a necessidade de justificar a sua rapidez, explicou ao professor que a soma seria o valor do produto de 50 pares de números por 101. Assim surge o número 5050. Valor ao qual, os colegas se renderam depois de meia hora de trabalho.
O raciocínio daquele aluno baseou-se na observação de que 1+100 = 2+98 = 3+97 = 4+96 = …= 50+51 = 101. Portanto, bastava adicionar 50 pares de números com o valor de 101.
Será que o leitor também já se tinha apercebido desta curiosidade? Experimente aplicar o mesmo raciocínio para determinar a soma de outra qualquer sequência do mesmo tipo. Em matemática estas sequências são conhecidas por progressões aritméticas - o termo seguinte, resulta da soma do termo anterior com um qualquer número que deve ser constante. Um exemplo de uma progressão aritmética é: 9, 12, 15, 18… em que a constante é 3. Querendo adicionar os 6 primeiros termos (9 + 12 + 15 + 18 + 21+ 24), de acordo com a descoberta de Gauss, é o mesmo que ter 33 + 33 + 33 = 3 x 33 = 99.
Este é um bom exemplo de como a matemática pode ser uma boa ferramenta para nos facilitar o trabalho, que em princípio, parecia ser exaustivo. Assim, tivesse a rapariga do hipermercado conhecimento disso e também ela teria a vida facilitada. A rapariga a que me refiro é a Catarina, funcionária numa empresa que vende salsichas enlatadas. Nunca gostou de matemática, e agora tem que dar conta, ao seu patrão, do número exacto de latas que utilizou na exposição feita no hipermercado.
As latas foram empilhadas de tal forma que cada uma está assente noutras duas latas, o que faz com que cada camada tenha menos uma lata que a camada de baixo.
O trabalho realizado pela Catarina é uma “parede” construída com as latas de salsichas distribuídas por 16 camadas, em que a última camada, a do cimo, tem 16 latas. Já fez 3 contagens e encontrou 3 números diferentes. Desesperada, pediu ajuda a uma colega para fazerem uma nova contagem, entretanto, foi encontrado um novo número. A sua amiga rapidamente se descartou daquela tarefa justificando-se que nunca tinha sido boa aluna a matemática.
É certo que Gauss já não vai poder ajudar a Catarina, mas deixou-nos a maior riqueza que se pode herdar - o conhecimento. É com base nesse conhecimento que conto com a solidariedade do leitor para ajudar a Catarina a determinar o número exato de latas que utilizou naquela construção.
Fonte: http://maismat.blogspot.com.br/2009/01/latas-em-progresso-aritmtica.html
Jogos de Memória
Segundo pesquisadores, crianças que têm uma memória de trabalho pouco eficiente têm dificuldades em Matemática. E considerando a recíproca, crianças que são pouco habilidosas em Matemática têm problemas com memória de trabalho. E mais, indivíduos sem dificuldades em Matemática tiveram melhor desempenho em atividades de memória de curto prazo verbal e viso-espacial. E o mais interessante, o desempenho das memórias de curto prazo verbal e viso-espacial, detectadas nos participantes, preveem o seu desempenho nas habilidades matemáticas.
Fonte: http://www.leoakio.com/jogos/calculadora-quebrada.swF

 O número
O número  é chamado de razão ou diferença comum da progressão aritmética.
é chamado de razão ou diferença comum da progressão aritmética.


 pode ser obtido por meio da formúla.
pode ser obtido por meio da formúla.
 é o primeiro termo;
é o primeiro termo;
 ou seja, que
ou seja, que  resulta que o n-ésimo termo é dado por:
resulta que o n-ésimo termo é dado por:
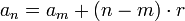

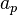 até
até  é calculada pela seguinte fórmula:
é calculada pela seguinte fórmula:

 a soma
a soma  de todos os termos dessa progressão pode ser escrita assim:
de todos os termos dessa progressão pode ser escrita assim:





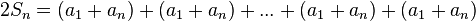
 pares de termos:
pares de termos: